Eliot Tron

Eliot Tron

he/him

Postdoc in Machine Learning and Geometry

Publications

You can also find my articles on my Google Scholar profile.

Journal Articles

The Geometry of Manifold Learning: Singular foliations via Deep Learning models

Published in ArXiv, 2026

This preprint explores the existence of singularity and smoothness of foliations associated with deep ReLU neural networks.

Recommended citation: Novelli, G., Tron, E., Latini, E., & Fioresi, R. (2026). "The Geometry of Manifold Learning: Singular foliations via Deep Learning models" (arXiv:2610.37370). arXiv. https://doi.org/10.48550/arXiv.2610.37370
Download Paper

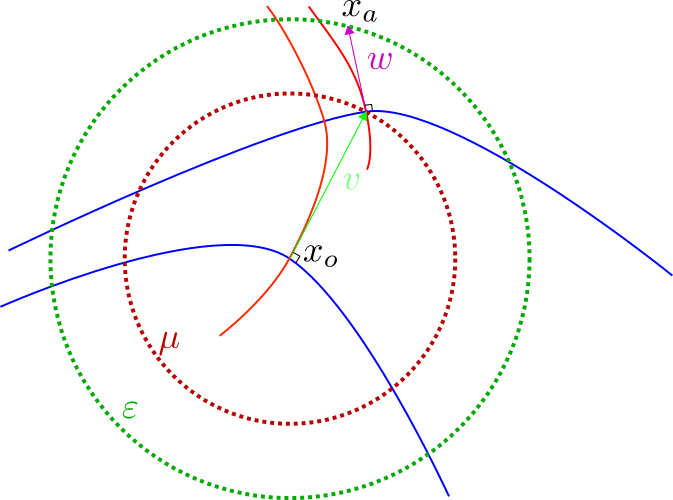
Cartan moving frames and the data manifolds

Published in Information Geometry, 2024

The study employs Cartan moving frames to analyze data manifolds and their curvature, offering insights into neural network outputs as an explainable AI tool.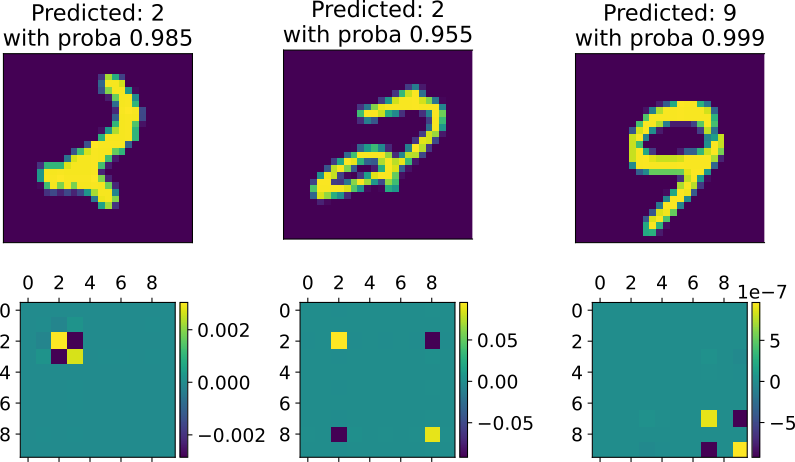

Recommended citation: Tron, Eliot; Fioresi, Rita; Couëllan, Nicolas; Puechmorel, Stéphane. "Cartan moving frames and the data manifolds." Info. Geo. (2024). https://doi.org/10.1007/s41884-024-00159-8.
Download Paper

Adversarial attacks on neural networks through canonical Riemannian foliations

Published in Machine Learning, 2024

This paper explores neural network robustness through Riemannian geometry, presenting a novel adversarial attack that highlights the role of curvature in the data space.

Recommended citation: Tron Eliot, Couëllan Nicolas, Puechmorel Stéphane. (2024). "Adversarial attacks on neural networks through canonical Riemannian foliations." Machine Learning.
Download Paper

Geometry of Singular Foliations and Learning Manifolds in ReLU Networks via the Data Information Matrix

Published in ArXiv, 2024

This study explores deep ReLU neural networks and manifold learning, uncovering a foliation structure that correlates with real data in high-dimensional spaces and shows potential for knowledge transfer.

Recommended citation: Tron, Eliot; Fioresi, Rita. (2024). "Geometry of Singular Foliations and Learning Manifolds in ReLU Networks via the Data Information Matrix." ArXiv preprint, https://doi.org/10.48550/arXiv.2409.07412.
Download Paper

PhD Thesis

Conference Papers

Equivariant Neural Networks and Differential Invariants Theory for Solving Partial Differential Equations

Published in Proceedings of The 41st International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, 2022

Equivariant Neural Networks for arbitrary symmetry groups to generalize Physics-Informed Neural Networks and approximate differential invariants.

Recommended citation: Lagrave, P.-Y.; Tron, E. Equivariant Neural Networks and Differential Invariants Theory for Solving Partial Differential Equations. Phys. Sci. Forum 2022, 5, 13. https://doi.org/10.3390/psf2022005013
Download Paper | Download Slides